1 Introduction

Dans un premier temps, nous allons importer les données dans R et ensuite les explorer pour mieux connaître la structure et les variables des données.

1.1 Sources des données

Les fichiers que nous allons importer sont présentés sur la page: Base de données accidents corporels de la circulation.

En cliquant sur les différentes rubriques, on peut télécharger les fichiers CSV. On a aussi un lien URL qui indique l’emplacement direct du fichier csv.

1.2 Fonctions d’import

Selon les types des données à importer, on peut utiliser des fonctions d’import des différents packages.

  • readr, data.table: fichiers csv
  • readxl: fichiers Excel
  • DBI: pour les bases de données
  • jsonlite: fichiers json
  • xml: pour lire les fichiers html

En l’occurrence on a des fichiers cvs.

Pour les fichiers cvs, on peut utiliser les fonctions suivantes:

  • read.csv ou read.csv2
  • fread du package data.table
  • read_csv du package readr

Certaines caractéristiques du fichier doivent être précisées lors de l’import, parfois, elles peuvent être détectées automatiquement:

  • le séparateur décimal
  • le séparateur des colonnes
  • le format des variables

2 Import des données

L’objectif de cette section est d’importer les données dans R.

2.1 Import d’un fichier csv

Pour importer les données, il faut préciser le lien du fichier à importer. On peut avoir plusieurs types de liens:

On peut afficher les premières lignes:

On peut remarquer un bug d’import pour la variable Num_Acc car c’est un grand nombre. Pour résoudre le problème, on a deux solution:

  • Soit on doit préciser l’option integer64 = "numeric" dans la fonction fread
  • Soit on précise que c’est une variable textuelle.

Dans un premier on va utiliser la première solution. En effet, la deuxième solution peut servir dans un cas général où on doit préciser la nature pour toutes les variabes du fichier.

2.2 Types de variables

Par défaut, un type de variable est attribué par la fonction d’import, mais il ne correspond pas toujours à ce qu’on souhaite. Ainsi, on peut préciser des options pour les préciser. On peut effectuer les étapes suivantes pour définir les types de variables lors de l’import.

  • Au lieu de préciser manuellement les types de variables, on peut utiliser la liste par défaut lors de l’import. On utilise donc la fonction d’import pour importer quelques lignes (pour cela, on peut utiliser l’option nrows).
  • Ensuite, on peut créer un vecteur qui contient les types de variables.
  • Pour les variables dont le type est à changer, on peut le faire à la main.
  • Le vecteur qui contient les types de variables final peut être utilisé pour l’import complet des bases.

2.3 Boucle d’import

On a quatre types de fichiers:

  • caracteristiques
  • vehicules
  • usagers
  • lieux

Pour chaque type de fichiers, on a un fichier par année. Ainsi, au lieu de préciser le lien pour chaque fichier, on peut créer une boucle.

3 Exloration des données

Après avoir importé les données, il est nécessaire d’explorer les données pour connaître les caractérististiques principales des bases.

3.1 Structure des données

On peut utiliser les différentes fonctions suivantes pour mieux connaître la structure des données:

  • str
  • summary et
  • describe du package Hmisc

3.1.1 Structure

## Classes 'data.table' and 'data.frame':   316854 obs. of  16 variables:
##  $ Num_Acc: num  201000000001 201000000002 201000000003 201000000004 201000000005 ...
##  $ an     : int  10 10 10 10 10 10 10 10 10 10 ...
##  $ mois   : int  6 8 9 9 10 2 2 5 6 7 ...
##  $ jour   : int  12 7 11 22 25 1 23 21 28 29 ...
##  $ hrmn   : int  1930 1000 1600 1630 1215 745 1515 1900 2300 615 ...
##  $ lum    : int  1 1 1 1 1 2 1 1 5 2 ...
##  $ agg    : int  2 2 1 2 2 1 2 1 2 2 ...
##  $ int    : int  1 1 1 1 1 1 1 1 1 2 ...
##  $ atm    : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ col    : int  6 6 5 6 2 4 1 5 6 5 ...
##  $ com    : int  52 477 11 477 52 550 51 320 51 51 ...
##  $ adr    : chr  "71 RUE JEAN JAURES" "Rue Nationale" "" "43 rue Nationale" ...
##  $ gps    : chr  "M" "M" "M" "M" ...
##  $ lat    : int  0 5051600 0 5051800 5050800 0 0 0 0 5054200 ...
##  $ long   : num  0 292000 0 292500 289700 ...
##  $ dep    : int  590 590 590 590 590 590 590 590 590 590 ...
##  - attr(*, ".internal.selfref")=<externalptr>

3.1.2 Résumé statistique

##     Num_Acc                   an             mois             jour     
##  Min.   :201000000001   Min.   :10.00   Min.   : 1.000   Min.   : 1.0  
##  1st Qu.:201100009835   1st Qu.:11.00   1st Qu.: 4.000   1st Qu.: 8.0  
##  Median :201200022074   Median :12.00   Median : 7.000   Median :16.0  
##  Mean   :201191312666   Mean   :11.91   Mean   : 6.676   Mean   :15.6  
##  3rd Qu.:201300039038   3rd Qu.:13.00   3rd Qu.:10.000   3rd Qu.:23.0  
##  Max.   :201400059854   Max.   :14.00   Max.   :12.000   Max.   :31.0  
##                                                                        
##       hrmn           lum             agg             int       
##  Min.   :   1   Min.   :1.000   Min.   :1.000   Min.   :0.000  
##  1st Qu.:1000   1st Qu.:1.000   1st Qu.:1.000   1st Qu.:1.000  
##  Median :1445   Median :1.000   Median :2.000   Median :1.000  
##  Mean   :1379   Mean   :1.911   Mean   :1.692   Mean   :1.727  
##  3rd Qu.:1810   3rd Qu.:3.000   3rd Qu.:2.000   3rd Qu.:2.000  
##  Max.   :2359   Max.   :5.000   Max.   :2.000   Max.   :9.000  
##                                                                
##       atm            col             com            adr           
##  Min.   :1.00   Min.   :1.000   Min.   :  1.0   Length:316854     
##  1st Qu.:1.00   1st Qu.:3.000   1st Qu.: 55.0   Class :character  
##  Median :1.00   Median :4.000   Median :116.0   Mode  :character  
##  Mean   :1.56   Mean   :4.228   Mean   :180.8                     
##  3rd Qu.:1.00   3rd Qu.:6.000   3rd Qu.:264.0                     
##  Max.   :9.00   Max.   :7.000   Max.   :987.0                     
##  NA's   :48     NA's   :9                                         
##      gps                 lat               long             
##  Length:316854      Min.   :      0   Min.   :     -510511  
##  Class :character   1st Qu.:      0   1st Qu.:           0  
##  Mode  :character   Median :4545025   Median :      107886  
##                     Mean   :3383247   Mean   :     7785201  
##                     3rd Qu.:4841248   3rd Qu.:      326502  
##                     Max.   :5564823   Max.   :612850000000  
##                     NA's   :167983    NA's   :167987        
##       dep       
##  Min.   : 10.0  
##  1st Qu.:330.0  
##  Median :640.0  
##  Mean   :569.1  
##  3rd Qu.:800.0  
##  Max.   :976.0  
##

3.1.3 Description

## caracteristiques 
## 
##  16  Variables      316854  Observations
## ---------------------------------------------------------------------------
## Num_Acc 
##            n      missing     distinct         Info         Mean 
##       316854            0       316854            1 201191312666 
##          Gmd          .05          .10          .25          .50 
##    160663393 201000015844 201000031686 201100009835 201200022074 
##          .75          .90          .95 
## 201300039038 201400028169 201400044011 
##                                                               
## Value      201000000000 201100000000 201200000000 201300000000
## Frequency         69379        66974        62250        58397
## Proportion        0.219        0.211        0.196        0.184
##                        
## Value      201400000000
## Frequency         59854
## Proportion        0.189
## ---------------------------------------------------------------------------
## an 
##        n  missing distinct     Info     Mean      Gmd 
##   316854        0        5    0.959    11.91    1.607 
##                                         
## Value         10    11    12    13    14
## Frequency  69379 66974 62250 58397 59854
## Proportion 0.219 0.211 0.196 0.184 0.189
## ---------------------------------------------------------------------------
## mois 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0       12    0.993    6.676    3.886        1        2 
##      .25      .50      .75      .90      .95 
##        4        7       10       11       12 
##                                                                       
## Value          1     2     3     4     5     6     7     8     9    10
## Frequency  24009 21083 25042 26003 27455 29413 27936 23404 29642 30239
## Proportion 0.076 0.067 0.079 0.082 0.087 0.093 0.088 0.074 0.094 0.095
##                       
## Value         11    12
## Frequency  27149 25479
## Proportion 0.086 0.080
## ---------------------------------------------------------------------------
## jour 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0       31    0.999     15.6    10.08        2        4 
##      .25      .50      .75      .90      .95 
##        8       16       23       28       29 
## 
## lowest :  1  2  3  4  5, highest: 27 28 29 30 31
## ---------------------------------------------------------------------------
## hrmn 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0     1437        1     1379      611      340      700 
##      .25      .50      .75      .90      .95 
##     1000     1445     1810     2020     2145 
## 
## lowest :    1    2    3    4    5, highest: 2355 2356 2357 2358 2359
## ---------------------------------------------------------------------------
## lum 
##        n  missing distinct     Info     Mean      Gmd 
##   316854        0        5     0.67    1.911    1.378 
##                                              
## Value           1      2      3      4      5
## Frequency  217678  18811  24393   2947  53025
## Proportion  0.687  0.059  0.077  0.009  0.167
## ---------------------------------------------------------------------------
## agg 
##        n  missing distinct     Info     Mean      Gmd 
##   316854        0        2    0.639    1.692    0.426 
##                         
## Value           1      2
## Frequency   97490 219364
## Proportion  0.308  0.692
## ---------------------------------------------------------------------------
## int 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0       10    0.648    1.727    1.189        1        1 
##      .25      .50      .75      .90      .95 
##        1        1        2        3        6 
##                                                                          
## Value           0      1      2      3      4      5      6      7      8
## Frequency      88 223139  38791  28120   4783   5026   9234   3165    344
## Proportion  0.000  0.704  0.122  0.089  0.015  0.016  0.029  0.010  0.001
##                  
## Value           9
## Frequency    4164
## Proportion  0.013
## ---------------------------------------------------------------------------
## atm 
##        n  missing distinct     Info     Mean      Gmd 
##   316806       48        9    0.478     1.56   0.9981 
##                                                                          
## Value           1      2      3      4      5      6      7      8      9
## Frequency  254813  33894   7319   2246   1786    732   3198  10408   2410
## Proportion  0.804  0.107  0.023  0.007  0.006  0.002  0.010  0.033  0.008
## ---------------------------------------------------------------------------
## col 
##        n  missing distinct     Info     Mean      Gmd 
##   316845        9        7    0.936    4.228     2.19 
##                                                            
## Value           1      2      3      4      5      6      7
## Frequency   29656  37764  89001   9743   9891 106641  34149
## Proportion  0.094  0.119  0.281  0.031  0.031  0.337  0.108
## ---------------------------------------------------------------------------
## com 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0      889        1    180.8    177.2        8       19 
##      .25      .50      .75      .90      .95 
##       55      116      264      447      549 
## 
## lowest :   1   2   3   4   5, highest: 926 933 934 938 987
## ---------------------------------------------------------------------------
## adr 
##        n  missing distinct 
##   265512    51342   159097 
## 
## lowest : -                        - LECLERC (AVENU DE LA D ----------, BESSE (PLACE ----------, MICHEL ANGE  ----------, VERDUN (DE 6
## highest: ZONE SOGARIS             ZOUAVE / BOISSIERE       ZU-RHEIN (136 RUE DU CH  ZUCCARELLI (PONT JEAN)   ZURICH (RUE DE)         
## ---------------------------------------------------------------------------
## gps 
##        n  missing distinct 
##   151246   165608        7 
##                                                            
## Value           A      G      M      R      S      T      Y
## Frequency    2741    848 145863   1735      2      2     55
## Proportion  0.018  0.006  0.964  0.011  0.000  0.000  0.000
## ---------------------------------------------------------------------------
## lat 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   148871   167983    68624    0.979  3383247  2008045        0        0 
##      .25      .50      .75      .90      .95 
##        0  4545025  4841248  4897360  4942963 
## 
## lowest :       0  404600  430900  438600  600000
## highest: 5115000 5115300 5118700 5121000 5564823
## ---------------------------------------------------------------------------
## long 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   148867   167987    85779    0.979  7785201 15536125  -204647  -110613 
##      .25      .50      .75      .90      .95 
##        0   107886   326502   538925   607732 
##                                                  
## Value                 0 520000000000 615000000000
## Frequency        148865            1            1
## Proportion            1            0            0
## ---------------------------------------------------------------------------
## dep 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##   316854        0      101    0.998    569.1    333.3       70      130 
##      .25      .50      .75      .90      .95 
##      330      640      800      930      940 
## 
## lowest :  10  20  30  40  50, highest: 971 972 973 974 976
## ---------------------------------------------------------------------------

Selon les besoins on peut utiliser ces différentes fonctions pour voir les types de variables, les exemples de valeurs, les résumés statistiques, les valeurs manquantes, les quantiles, etc.

On peut aussi créer une boucle pour les quatre bases.

3.2 Valeurs manquantes

Il est important d’analyser les valeurs manquantes dans les données.

3.2.1 Visualisation simple

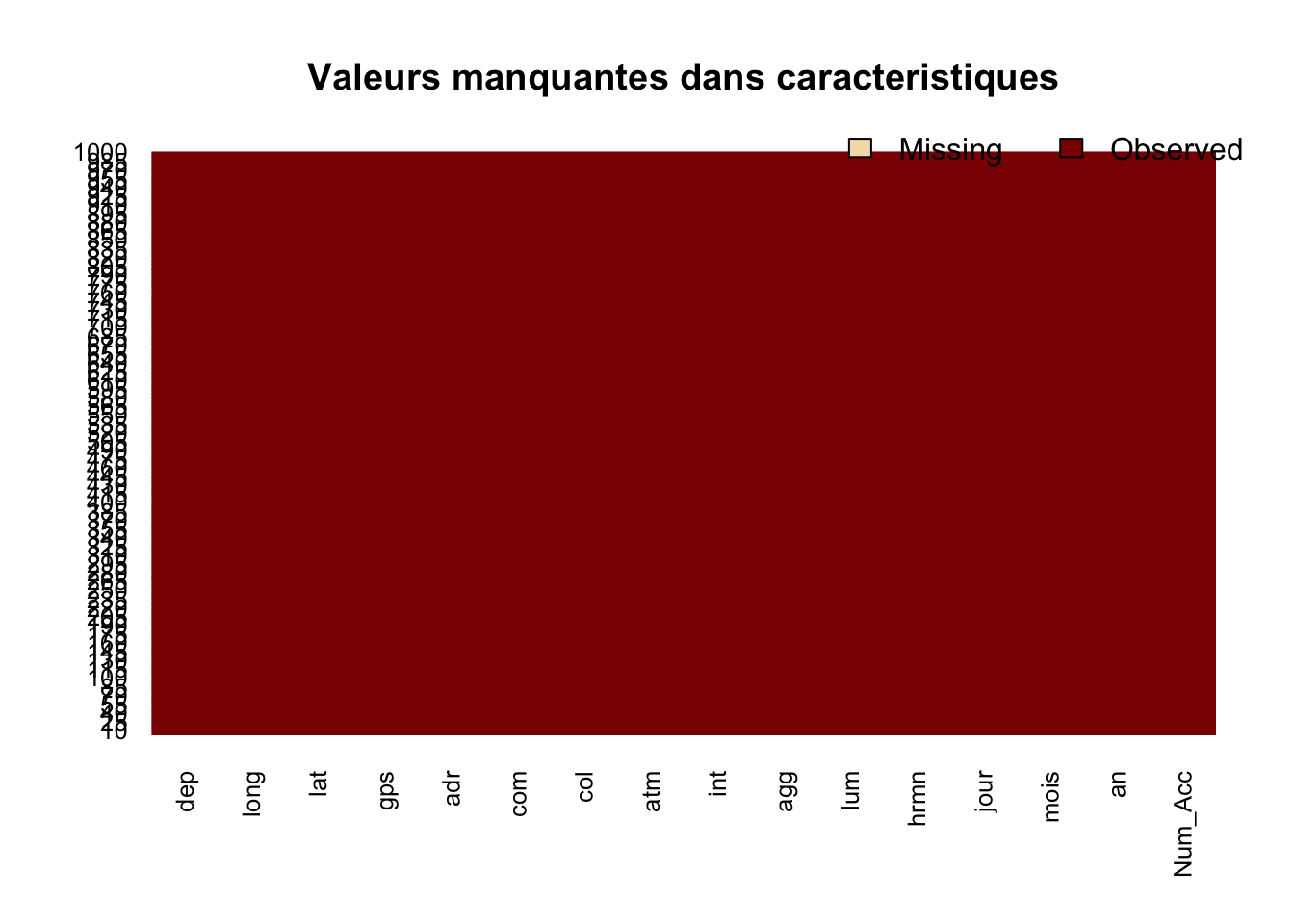
On peut créer une visualisation pour représenter les valeurs manquantes. Comme les bases sont grandes, on affiche uniquement les 1000 premières lignes.

  • De façon très visuelle, on voit pour chacune des variables les valeurs manquantes symbolisées par des lignes jaunes.
  • Par exemple dans la base caractéristiques, on voit qu’il y a beaucoup de valeurs manquantes parmi les 1000 premières lignes, pour les variables long et lat.

3.2.1.1 caracteristiques

NULL

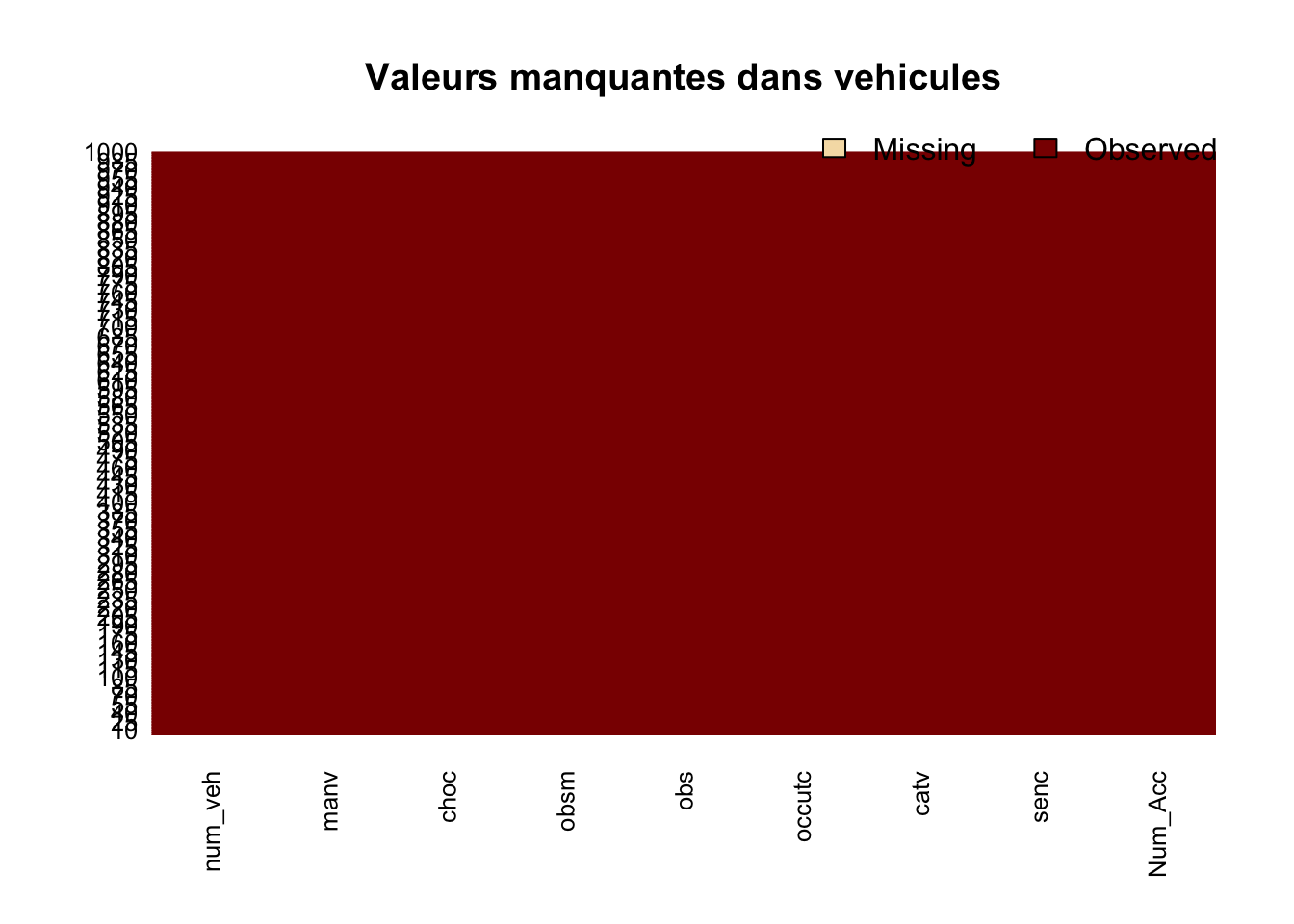
3.2.1.2 vehicules

NULL

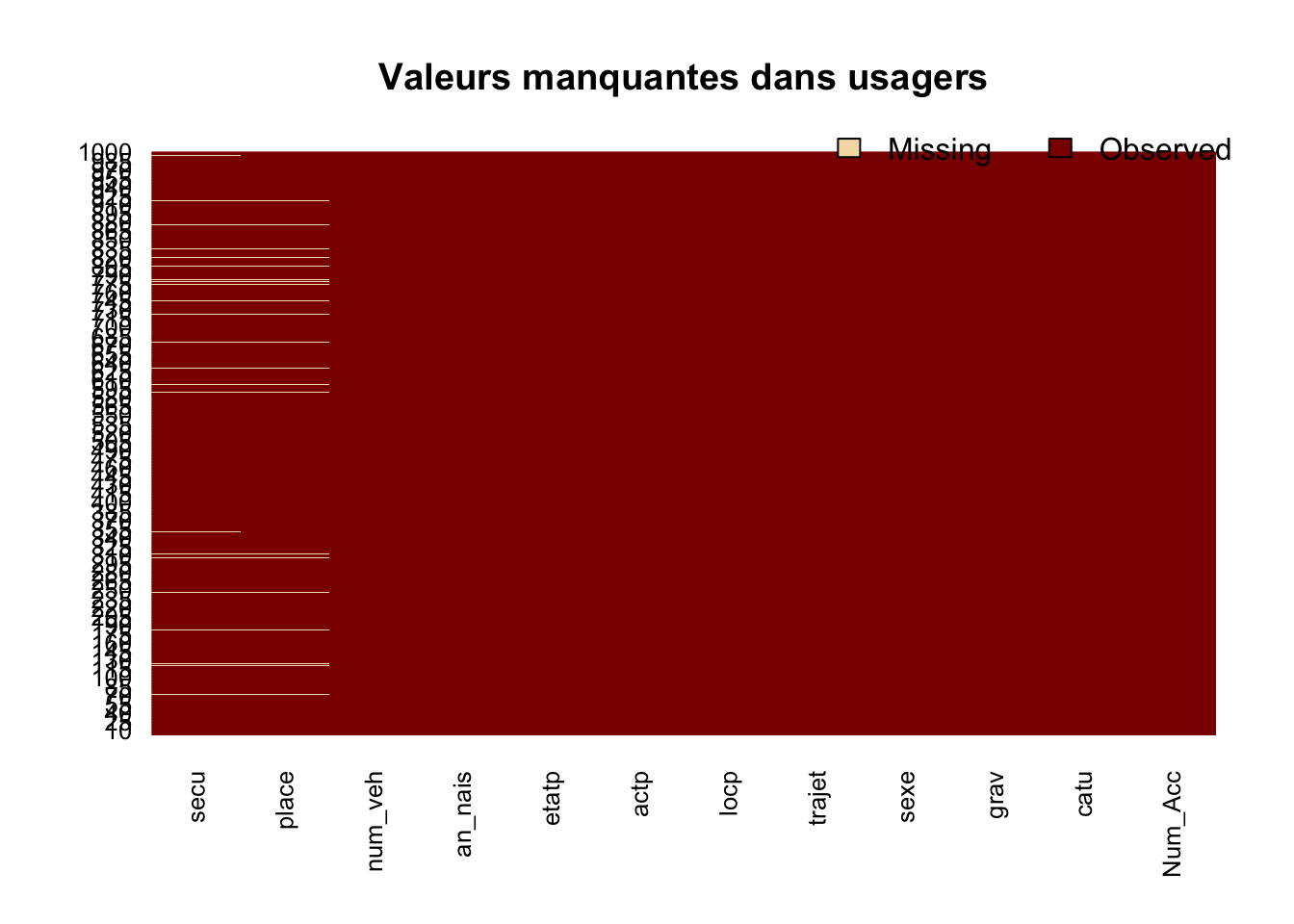
3.2.1.3 usagers

NULL

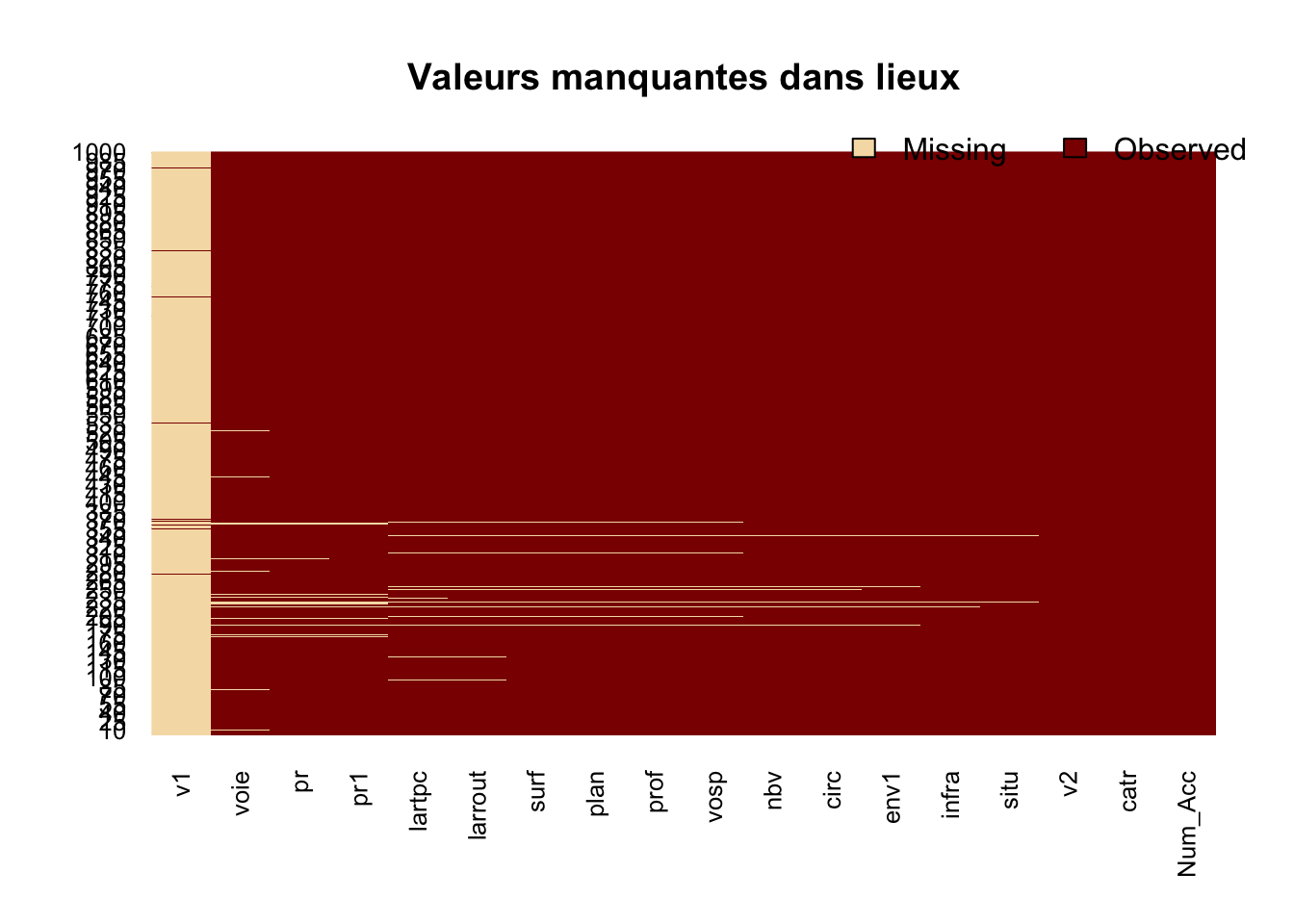
3.2.1.4 lieux

NULL

3.2.2 Visualisation avec type

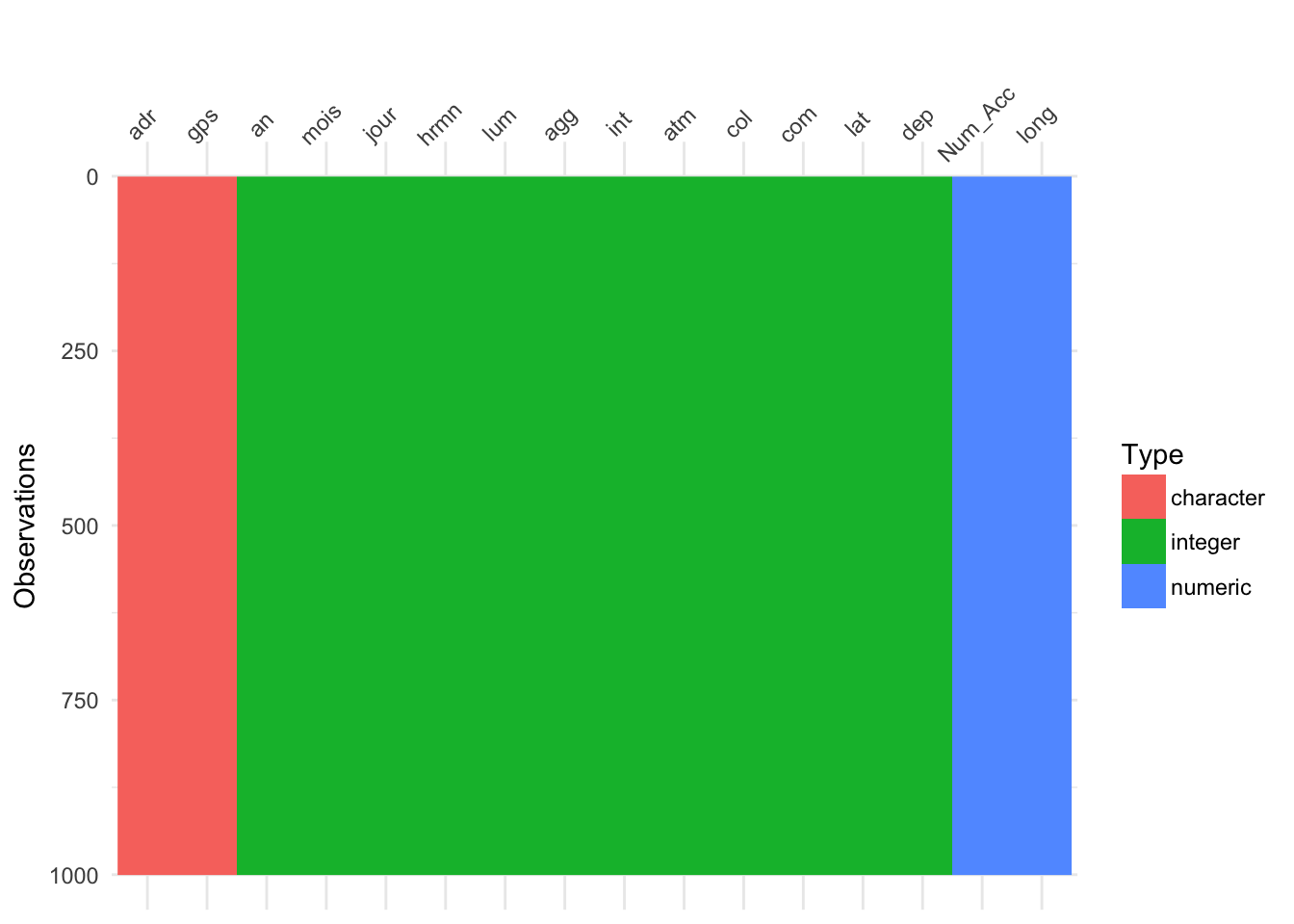
On peut créer une visualisation pour mieux se rendre compte de la structure des données et les valeurs manquantes. Avec les différentes couleurs, cela rend l’exploration plus visuelle.

  • Pour les valeurs manquantes, on voit des traits gris.
  • En plus de ça, par rapport à la méthode visualisation précédente, on voit des couleurs différentes pour distinguer les différents types de variables
    • character en rouge
    • date en maron
    • factor en vert
    • integer en bleu turquois
    • numeric en bleu ciel

3.2.2.1 caracteristiques

3.2.2.2 vehicules

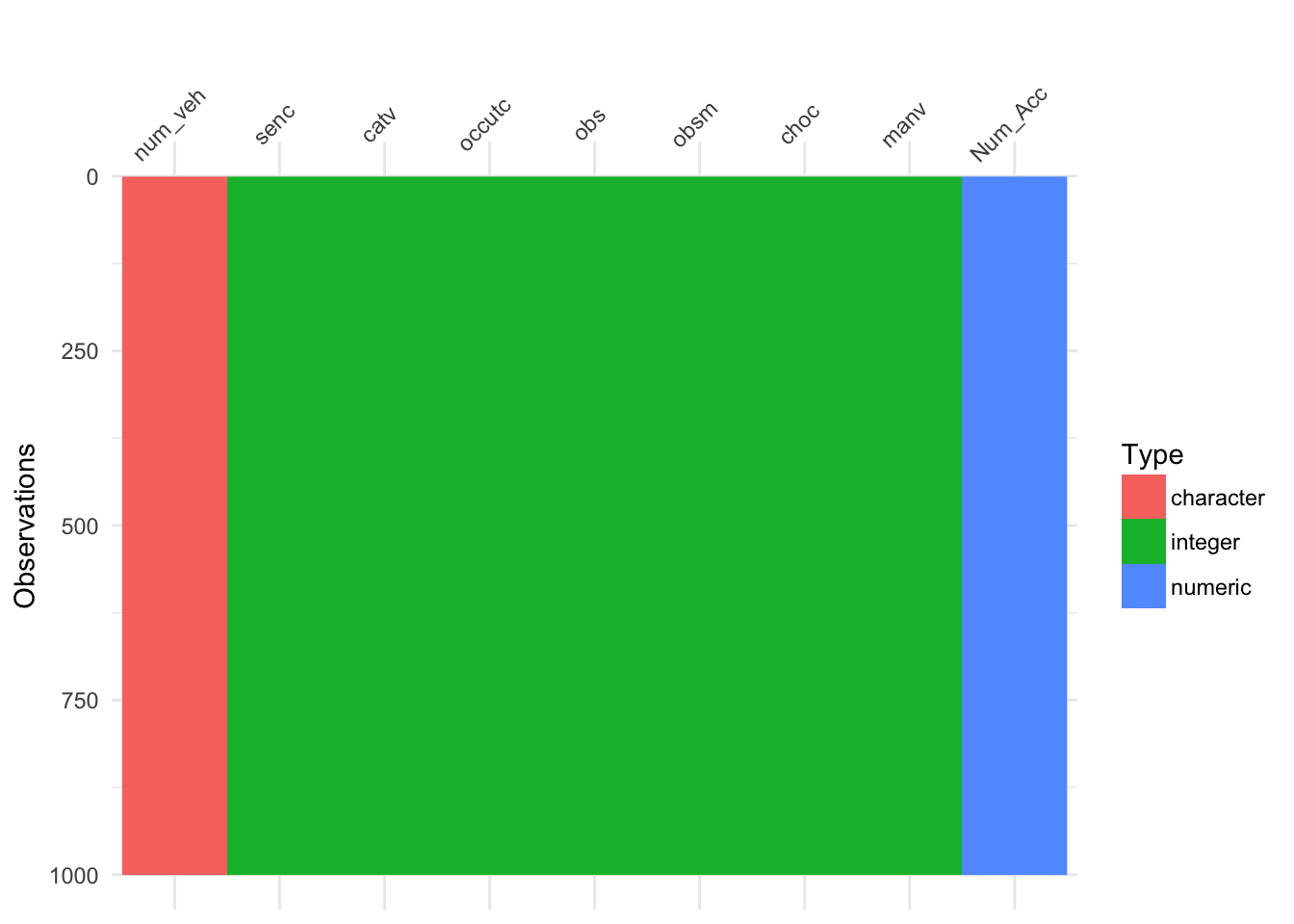
3.2.2.3 usagers

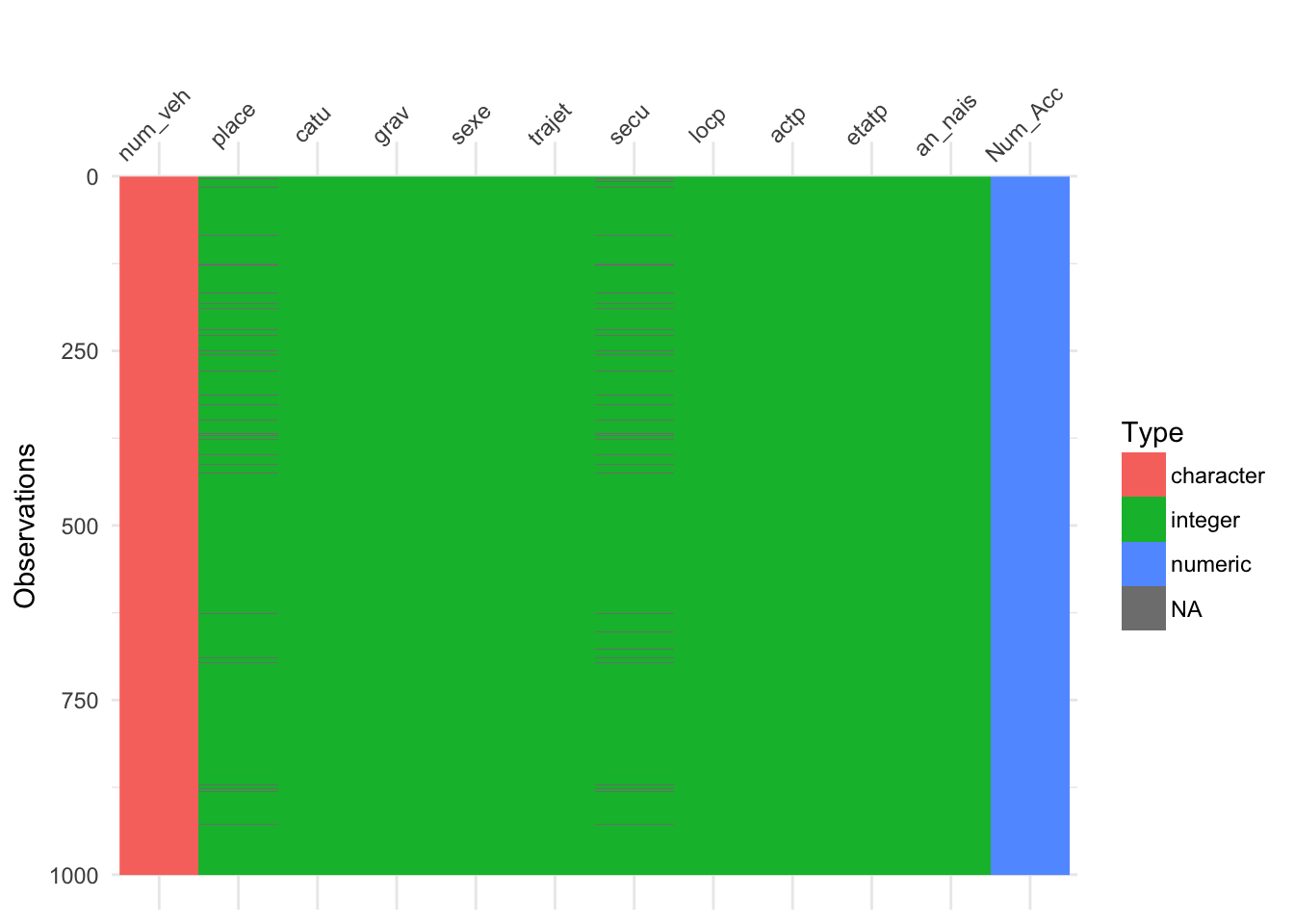
3.2.2.4 lieux

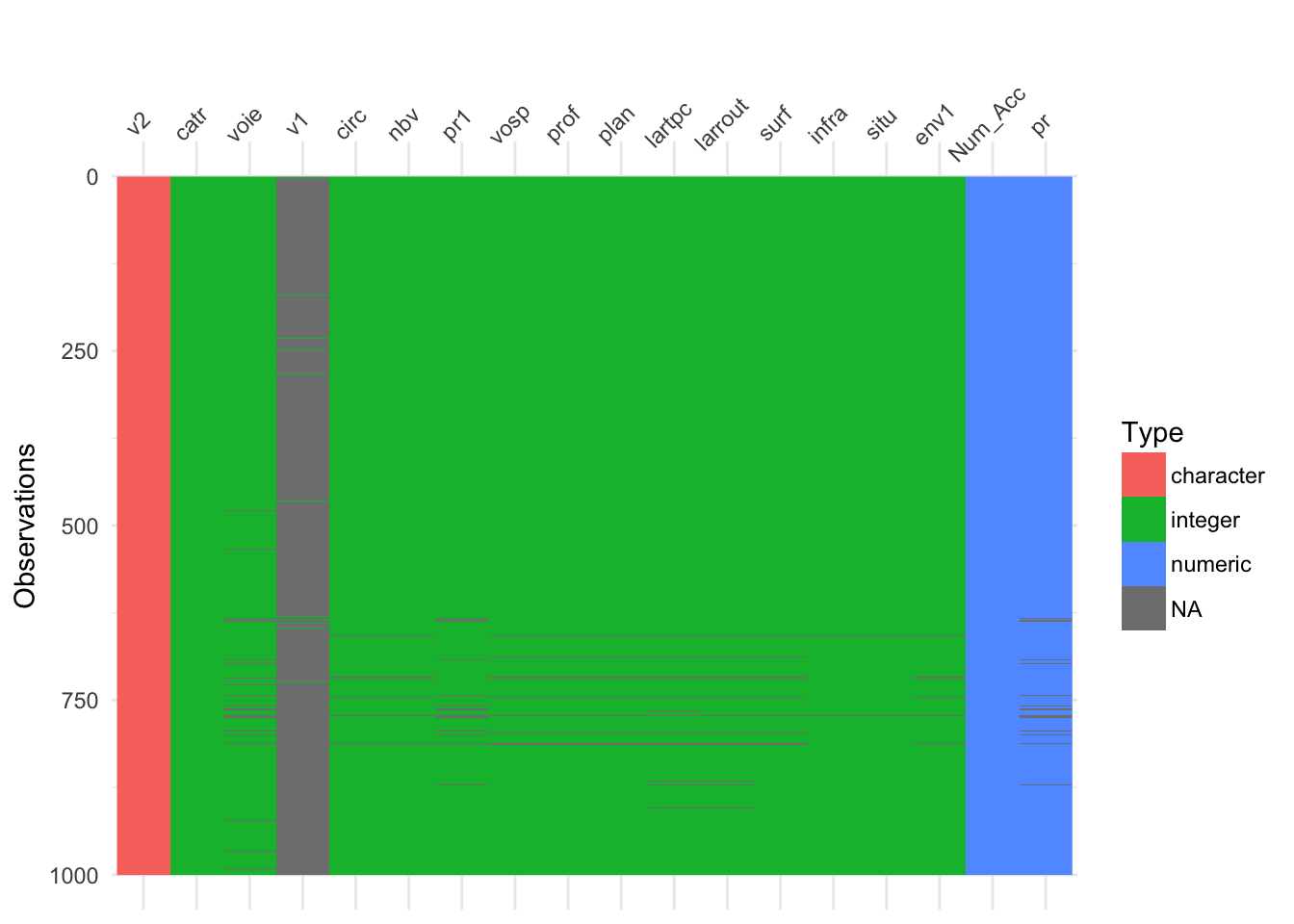
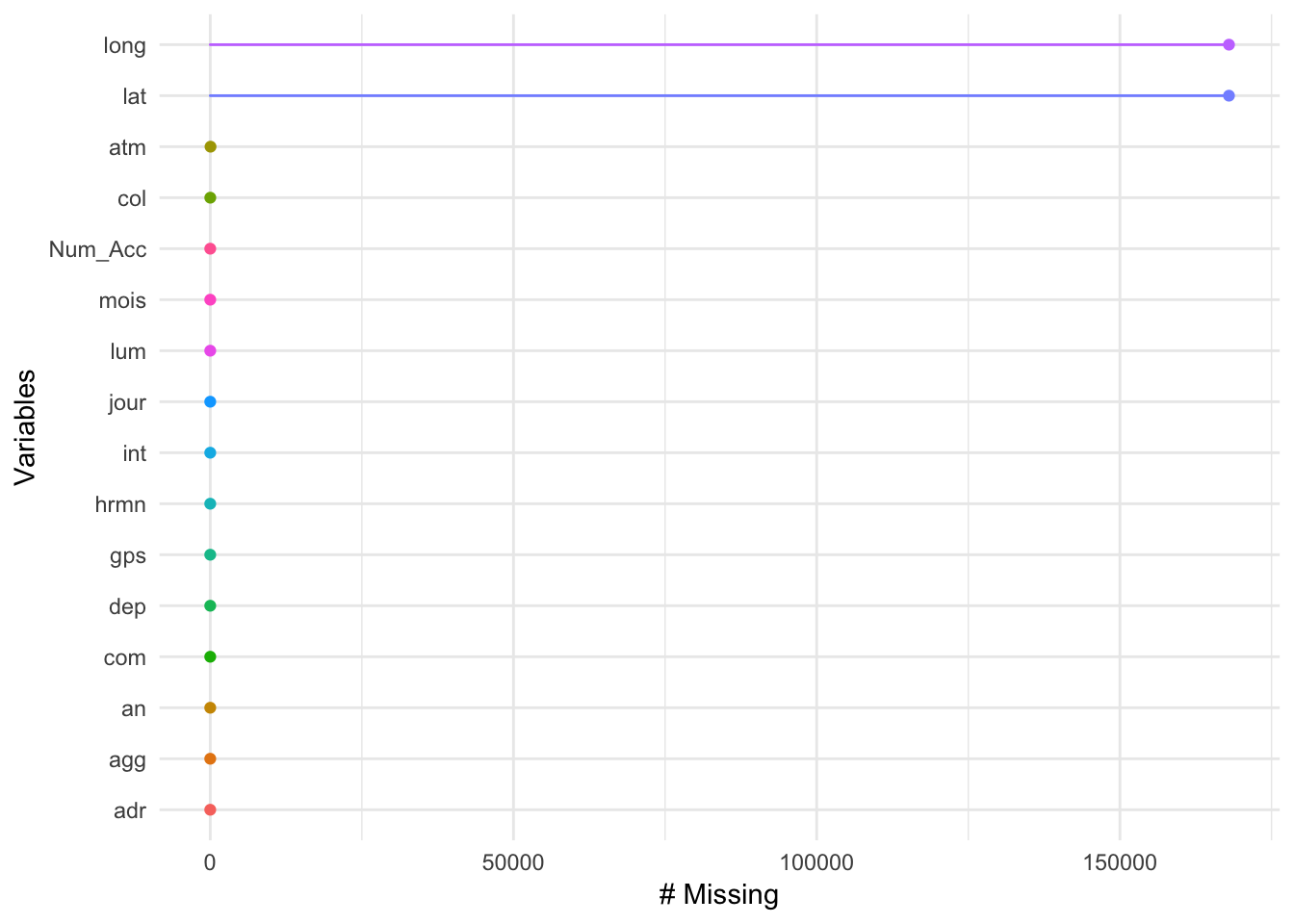
3.3 Comptage des valeurs manquantes

Dans les graphique précedents, on a réduit le nombre de ligne exploré, si on veut une statistique exacte des valeurs manquantes, on peut compter les nombres de valeurs manquates par variable.

3.3.1 Comptage simple

3.3.1.1 caracteristiques

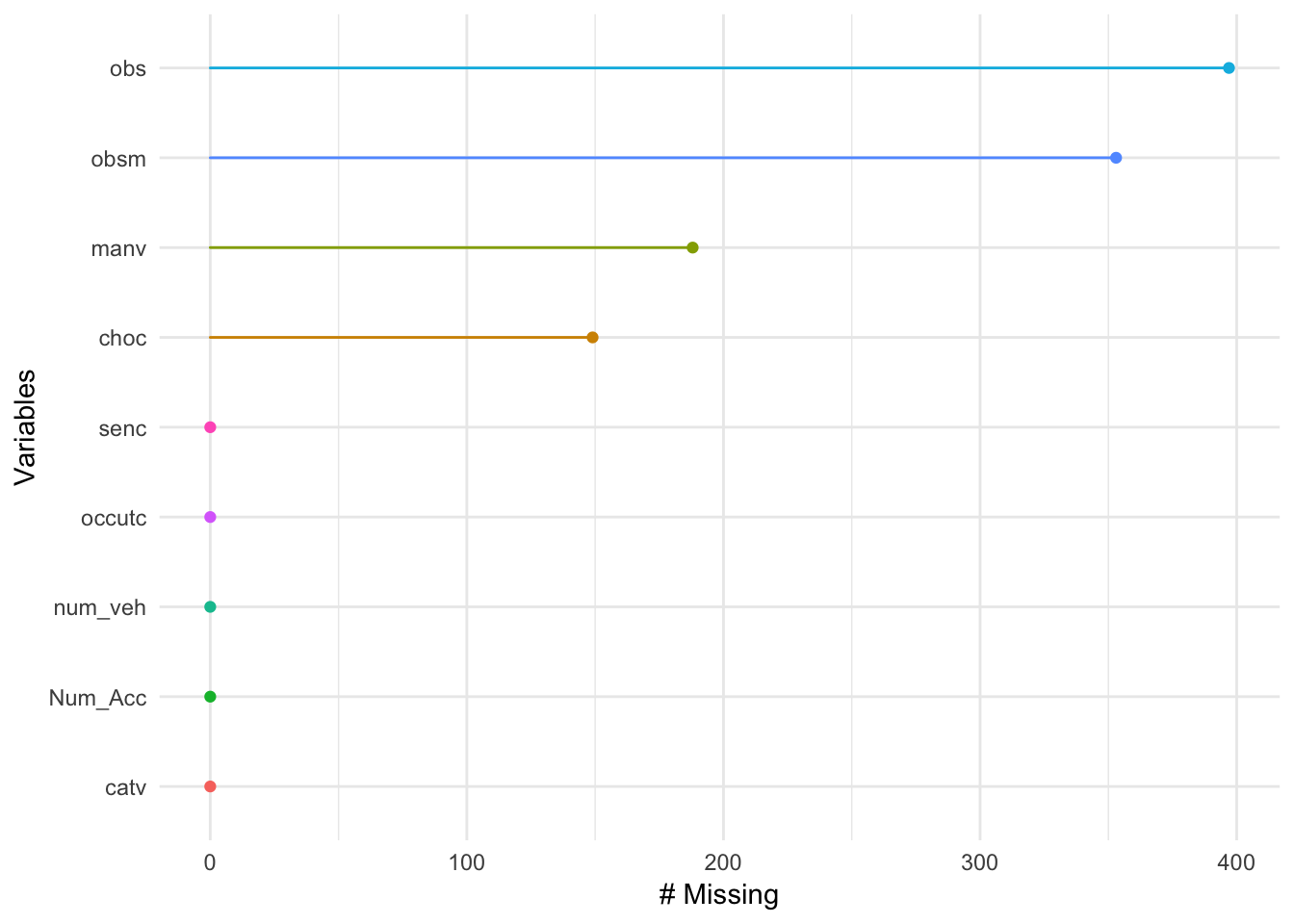
3.3.1.2 vehicules

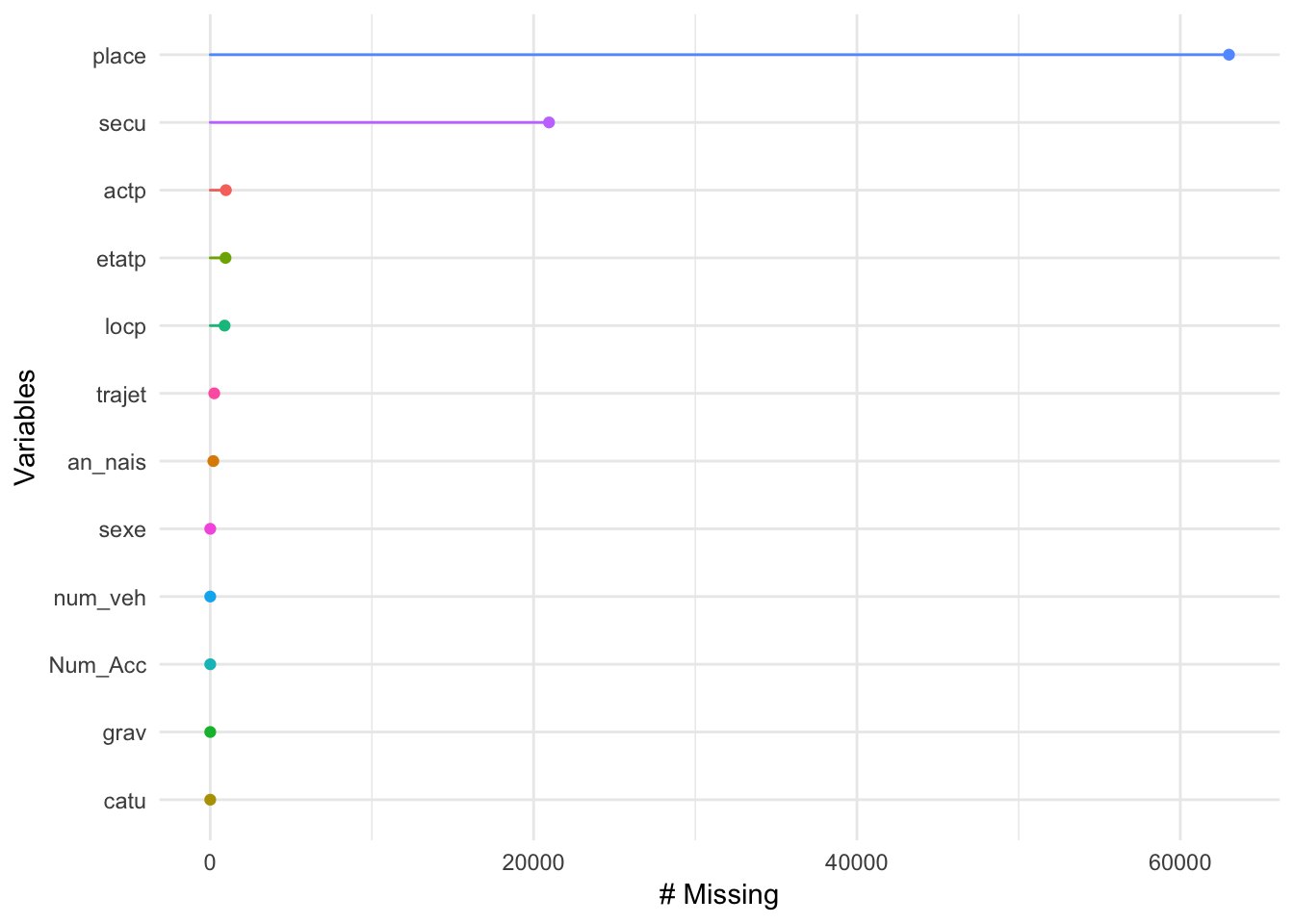
3.3.1.3 usagers

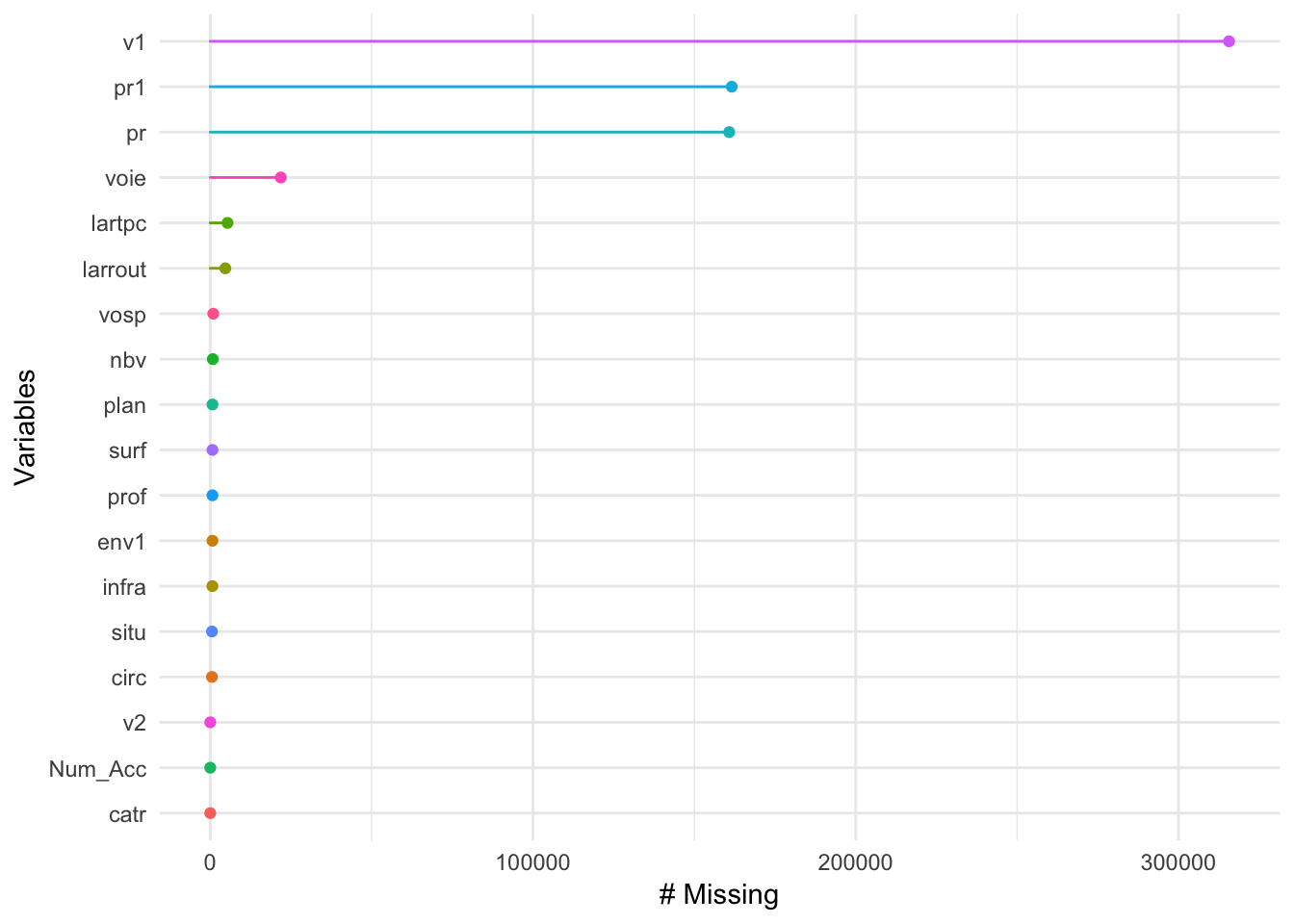
3.3.1.4 lieux

3.3.2 Comptage croisé

On peut aussi créer un tableau de valeurs.

Pour des besoins précis lors qu’on aura une meilleure connaissance des données, on peut créer un résumé des valeurs manquantes d’une variable en faisant des groupes d’observations à partir d’une autre variable.

Copyright © 2017 Blog de Kezhan Shi